C Program to find the points using DDA algorithm
Algorithm:-
Suppose at step i, the pixels is (xi,yi)
The line of equation for step i
yi=mxi+b......................equation 1
yi=mxi+b......................equation 1
Next value will be
yi+1=mxi+1+b.................equation 2
m =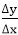
yi+1=mxi+1+b.................equation 2
m =
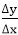
yi+1-yi=∆y.......................equation 3
yi+1-xi=∆x......................equation 4
yi+1=yi+∆y
∆y=m∆x
yi+1=yi+m∆x
∆x=∆y/m
xi+1=xi+∆x
xi+1=xi+∆y/m
yi+1-xi=∆x......................equation 4
yi+1=yi+∆y
∆y=m∆x
yi+1=yi+m∆x
∆x=∆y/m
xi+1=xi+∆x
xi+1=xi+∆y/m
Case1: When |M|<1 assume="" sub="" that="" then="" x="">1
<1 assume="" sub="" that="" then="" x="">
<1 assume="" sub="" that="" then="" x="">
yi+1=y1+m, x=x+1
Until x = x2
Case2: When |M|<1 assume="" sub="" that="" then="" y="">1
<1 assume="" sub="" that="" then="" y="">
<1 assume="" sub="" that="" then="" y="">
xi+1=
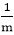 , y=y+1
, y=y+1#include<stdio.h>
#include<math.h>
int main()
{
int x1,x2,y1,y2;
float x,y;
int i=1,roundx,roundy,step;
float dx,dy,xinc,yinc,xnew,ynew;
printf("Enter the end points first\n");
scanf("%d%d",&x1,&y1);
printf("Enter the end points second\n");
scanf("%d%d",&x2,&y2);
printf("step\txold\tyold\txnew\tynew\tround(x),round(y)");
dx=(x2-x1);
dy=y2-y1;
if(abs(dx)>abs(dy))
{
step=abs(dx);
}
else
{
step=abs(dy);
}
x=x1;
y=y1;
xinc=dx/step;
yinc=dy/step;
xnew=(x+xinc);
ynew=(y+yinc);
roundx=roundl(xnew);
roundy=roundl(ynew);
printf("\n%d\t%.2f\t%.2f\t%.2f\t%.2f\t(%d,%d)",i,x,y,xnew,ynew,roundx,roundy);
do
{
i++;
x=xnew;
y=ynew;
xnew=(x+xinc);
ynew=(y+yinc);
roundx=roundf(xnew);
roundy=roundf(ynew);
printf("\n%d\t%.2f\t%.2f\t%.2f\t%.2f\t(%d,%d)",i,x,y,xnew,ynew,roundx,roundy);
}
while(i<step);
}
C Programming Languages | C Program to draw lines using DDA algorithm
#include<stdio.h>
#include<math.h>
#include<graphics.h>
int main()
{
int gd=DETECT,gm;
initgraph(&gd,&gm,"");
int x1,x2,y1,y2;
float x,y;
int i=1,roundx,roundy,step;
float dx,dy,xinc,yinc,xnew,ynew;
printf("Enter the end points first\n");
scanf("%d%d",&x1,&y1);
printf("Enter the end points second\n");
scanf("%d%d",&x2,&y2);
dx=(x2-x1);
dy=y2-y1;
if(abs(dx)>abs(dy))
{
step=abs(dx);
}
else
{
step=abs(dy);
}
x=x1;
y=y1;
xinc=dx/step;
yinc=dy/step;
xnew=(x+xinc);
ynew=(y+yinc);
roundx=roundl(xnew);
roundy=roundl(ynew);
putpixel(roundx,roundy,RED);
do
{
i++;
x=xnew;
y=ynew;
xnew=(x+xinc);
ynew=(y+yinc);
roundx=roundf(xnew);
roundy=roundf(ynew);
putpixel(roundx,roundy,RED);
}
while(i<step);
getch();
closegraph;
}
